Expanding Rods(LightOj-1137)
Problem statement
Here we are given a solid rod of length L that expands to length L’ and creates an arch shape with the original shape of the rod. Our task is to compute the distance by which the center of the rod is displaced. The problem could be easily visualized with the given picture in the problem statement. Let’s assume the straight rod AB is placed inside a circle and the arch shaped rod AB arch is on the perimeter of this circle. We can visualize it like this -
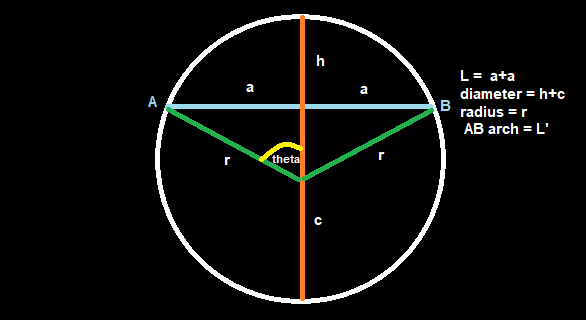
Here h+c is the diameter of the circle. our aim is to find this h. This line have intersected our original rod shape line AB at the centre and so we can say that L = 2a or a = L/2. Now, from the Intersecting Cord Theorem we get -
Let D be the diameter of this circle and r be the radius. Hence,
Deviding D by 2 we get the radius
Let’s find out theta as shown in the circle. As theta is an angle in a parpendicular triangle and we know value of two of the sides r and a, we can easily calculate it.


Now lets’s see - we have radius of the circle r, we have an angle theta, if we double theta we get the angle for arch AB. So, we can calculate the arch length using formula. At first we will calculate L’ as given in the problem statement.
We can now apply binary search/bisection method using h as a key or mid value, lower bound as 0 and higher bound as L/2 (as it is said- Input data guarantee that no rod expands by more than one-half of its original length, so h must be smaller than L/2). For each corresponding value of h, S will be determined and compared to L’. If S is greater that L’ that means we need to lower the value of h. If S is lesser that L’ that means we need to increase the value of h. After some careful iteration we will get our required value of h within O(log2(L/2)) complexity for each testcase.
Source Code
#include<bits/stdc++.h>
#define EPS 1e-7
using namespace std;
int main()
{
int T;
double L,n,C;
cin >> T;
for(int t=1;t<=T;t++)
{
cin >> L >> n >> C;
double L_prime = (1.0+n*C)*L;
double a = L/2.0,s=L_prime;
double h,r,theta,temp_s,low=0,high=L/2.0;
while(high-low>EPS)
{
h = (low+high)/2.0;
r = ((L*L)/(8.0*h)) + (h/2.0);
theta = 2.0*asin(a/r);
temp_s = r*theta;
if(temp_s>=s)
high=h;
else low=h;
}
cout << "Case " << t << ": " << setprecision(7) << fixed << low << endl;
}
return 0;
}
